Polyedrische Strukturen
Polyeder — Körper, die aus ebenen Teilen gebildet werden — spielen bei der Herstellung aus ebenen Materialien eine wichtige Rolle. Bereits Platon hatte die fünf möglichen völlig regelmäßigen Körper beschrieben und sie den Elementen zugeordnet. Kepler studierte polyedrische Strukturen in seiner Weltharmonik, verwendete sie zur Erzeugung dichter Raumpackungen und um die Planetenbahnen zu beschreiben. Ausgangspunkt unseres Seminars waren Überlegungen zu (halb-)regelmäßigen Polyedern. Das Prinzip der Dualität erweist sich als ein wirkungsvolles geometrisches Werkzeug, um von den halbregelmäßigen Polyedern zu solchen zu gelangen, die aus lauter gleichen aber unregelmäßigen Vielecken gebildet werden.
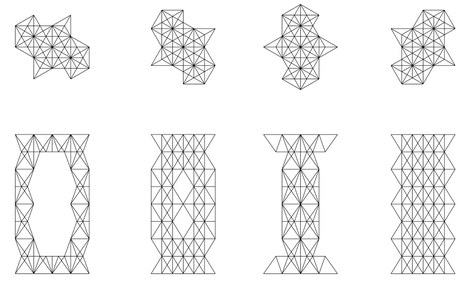
Arutiun Papikian setzte sich mit polyedrischen Tragstrukturen auseinander. Nach einer Studie der Vorgehensweisen von Richard Buckminster Fuller und Konrad Wachsmann entwickelte er eine triangulare Tragstruktur aus irregulären Polyedern, nennt sie Ж-Struktur. Sie soll durch ihre geometrische Ordnung sowohl horizontal, vertikal als auch lateral eingesetzt werden können. Aus unterschiedlichen Seiten betrachtet, werden die vielfältigen Möglichkeiten, dieser polyedrischen Struktur deutlich.

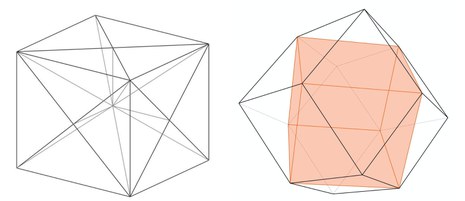
Philipp Lorenz gelang die Umstülpung des Würfels durch dessen Zerlegung in gleiche Teile. Er zerlegte den Würfel in kongruente Tetraeder und fügte diese 24 Glieder in einem Gelenkring zusammen. Der Kubus X von Fred Voss 2006 entwickelt, wurde so zum Kubus X2, indem er weiter unterteilte, jeder Würfelseite mittels zwei Flächendiagonalen. Bei der Umstülpung des Würfels zum Rhombendodekaeder mit innenliegendem Hohlraum in Form des Würfels sind viele Zwischenstationen als Formvariationen möglich.


