Pattern Matters
Lecturers: Akad Dir. Cornelie Leopold, Dipl.-Ing. Viyaleta Zhurava

The study of patterns is the basis for many design tasks. We chose the English word pattern, because this fits better than the German words Muster, Flächenornament, Parkettierung, Anordnungen ... and includes these different aspects. Parquetry means the gapless and overlap-free overlapping of congruent figures, which, starting from basic geometric shapes, can also become figurative. Spatial packings are the spatial counterpart of planar patterns. 3D-packages or 3D-tessellations by means of polyhedra form the basis for spatial arrangements and compositions. Through transformations and metamorphoses, transitions between patterns and spatial compositions are possible. This also allows design processes to be mediated from regular to irregular patterns.


In architecture, from urban design to building structure to support structure, these geometric relationships are built upon. Therefore, we also analyzed corresponding architectural examples.


From 2D and 3D patterns as well as their transformations or metamorphoses, the student Pattern Matters projects emerged as a digital and materialized composition.


Working with the 3D modeling software Rhinoceros was used as a suitable tool. In a voluntary block course with Eva Hagen before the beginning of the semester the students were taught the basics or advanced students will receive extended input. Parametric design using Grasshopper was also integrated.
 Guest lecture
Guest lecture
Architect - Univ. Lecturer
Ornamental Art & Design, Vienna
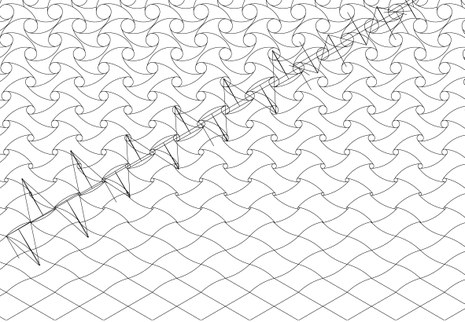
Design and Analysis of Parquet Deformations
Tuesday 04 May, 2021, 10 Uhr
Lecture in German
 Workshop
Workshop
Ph.D. Researcher in the Centre for Studies of Architecture and Urbanism, Faculty of Architecture, University of Porto, Portugal
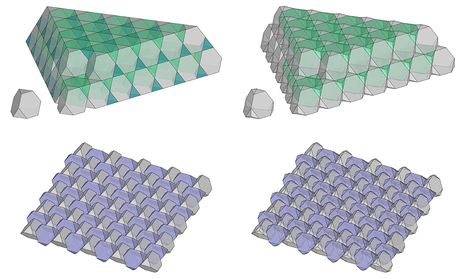
Tessellating and Interlocking in Patterns
Tuesday 18 May, 2021, 10 Uhrin Zoom
Having understood the connections between 2D and 3D tessellations, we addressed the concept of topological interlocking and learned how the interlocked assemblies of convex regular polyhedra are obtained.
With the knowledge of some basic rules, the participants then were able to model, on their own, interesting patterns with tessellated or interlocked polyhedra.

